Олимпиадная задача Гальперина: треугольники после разрезов — все ли тупоугольные?
Задача
Остроугольный треугольник разрезали прямолинейным разрезом на две (не обязательно треугольные) части, затем одну из этих частей – опять на две части, и так далее: на каждом шаге выбирали любую из уже имеющихся частей и разрезали её (по прямой) на две. Через несколько шагов оказалось, что исходный треугольник распался на несколько треугольников. Могут ли все они быть тупоугольными?
Решение
Решение 1: У "нетупоугольного" треугольника есть три нетупых угла. Достаточно доказать, что при прямолинейном разрезании многоугольника, имеющего (по крайней мере) три нетупых угла, один из двух получившихся многоугольников обладает тем же свойством. Действительно, тогда после каждого шаге (в частности, после последнего) имеется часть с этим свойством. В конце же остались одни треугольники, значит, в одном из них все углы – не тупые.
Итак, пусть есть многоугольник с тремя нетупыми углами. Разрежем его. На каждом конце разреза добавляется еще по крайней мере один нетупой угол (если разрез рассек один из нетупых углов, то оба получившихся из него угла – острые). Поэтому в двух получившихся многоугольниках – не менее пяти нетупых углов, следовательно, в одном из них – не менее трёх.
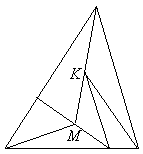
Решение 2: Пусть в результате получилось n треугольников. Сумма их углов равна 180n°. Но эту сумму можно подсчитать и по-другому. Рассмотрим все точки, являющиеся вершинами этих треугольников. Разобьём эти точки на три типа. К первому отнесём те точки, в которых сходящиеся в них углы треугольников составляют полный угол (как точка М на рисунке). Ко второму – точки, в которых эти углы составляют развёрнутый угол (как точка К). Наконец, к третьему типу отнесём вершины исходного треугольника. Если имеется m точек первого и k точек второго типа, то общая сумма углов равна 360m° + 180k° + 180°. Отсюда n = 2m + k + 1.
Ответ
Не могут.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь