Олимпиадная задача по планиметрии и стереометрии: проекции куба для 10-11 классов
Задача
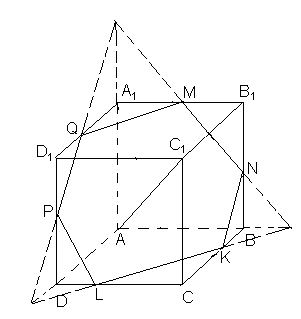
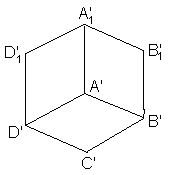
В кубе АВСDА1В1С1D1 площадь ортогональной проекции грани АА1В1В на плоскость, перпендикулярную диагонали АС1, равна 1.
Найдите площадь ортогональной проекции куба на эту плоскость.
Решение
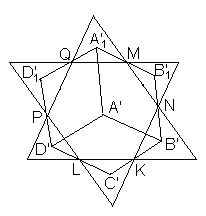
Первый способ. Выберем плоскость проекции так, чтобы она проходила через центр куба. Сечением куба этой плоскостью является правильный шестиугольник MNKLPQ (рис. слева). Проекцией куба на эту плоскость является шестиугольник A'1B1B'C'D'D'1 (рис. в центре), вершины которого являются центрами правильных треугольников, построенных на сторонах шестиугольника MNKLPQ, поэтому полученный шестиугольник также является правильным, причём вершины A и C1 куба проектируются в его центр. Проекцией грани АА1В1В является параллелограмм A'A'1B'1B'. Его площадь в три раза меньше площади проекции куба.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь