Олимпиадная задача по планиметрии: наименьший периметр треугольника РКМ для 8-9 класса
Задача
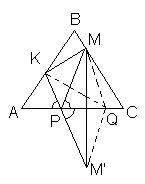
Дан равносторонний треугольник АВС. Точка К – середина стороны АВ, точка М лежит на стороне ВС, причём ВМ : МС = 1 : 3. На стороне АС выбрана точка P так, что периметр треугольника РКМ – наименьший из возможных. В каком отношении точка Р делит сторону АС?
Решение
Рассмотрим точку M', симметричную точке М относительно прямой АС. Согласно решению задачи 152489 Р – точка пересечения KМ' и АС. Так как
∠MPC = ∠M'PC = ∠KPA, то треугольники МРС и КPA подобны по двум углам. Следовательно, AP : CP = АК : CM = ½ : ¾ = 2 : 3.
Ответ
2 : 3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет