Олимпиадная задача по планиметрии для 8–10 классов: точки A₁, B₁, C₁ и пересечение прямых
Задача
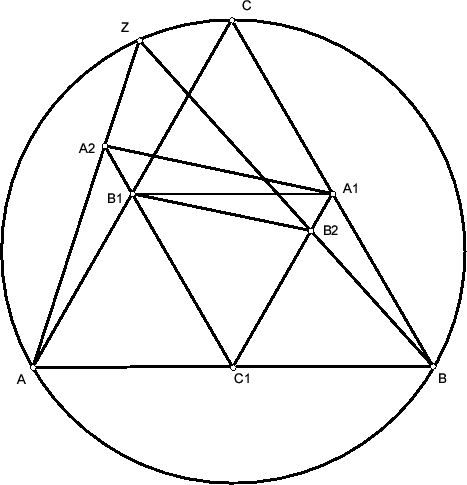
Точки A1, B1, C1 – середины сторон правильного треугольника ABC. Три параллельные прямые, проходящие через A1, B1, C1, пересекают, соответственно, прямые B1C1, C1A1, A1B1 в точках A2, B2, C2. Доказать, что прямые AA2, BB2, CC2 пересекаются в одной точке, лежащей на описанной окружности треугольника ABC.
Решение
Пусть Z – точка пересечения AA2 и BB2. Так как точки B и B1 симметричны относительно прямой A1C1, ∠ABZ = ∠C1BB2 = ∠B2B1C1. Аналогично
∠BAZ = ∠A2A1C1. Так как прямые AA2 и BB2 параллельны, ∠A2A1C2 = ∠B1B2C, следовательно, ∠AZB = ∠B1C1B2 = ∠C, то есть точка Z лежит на описанной окружности Ω треугольника ABC.
Аналогично доказывается, что AA2 и CC2 пересекаются в точке, лежащей на Ω, то есть в той же точке Z.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь