Олимпиадная задача по планиметрии: равнобедренные треугольники и невозможность разрезания

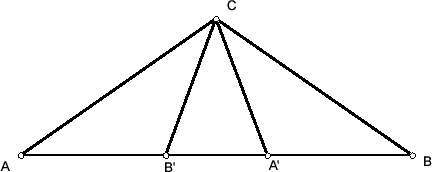
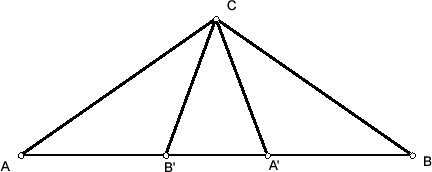
  Остроугольный треугольник можно разрезать на три равнобедренных с равными боковыми сторонами радиусами описанной окружности. Если треугольник ABC – тупоугольный (C – тупой угол), то возьмём на стороне AB такие точки A', B', что  AB' = B'C = CA' = A'B,  и разрежем треугольник на треугольники AB'C, A'B'C и A'BC (см. рис.).

  Докажем, что прямоугольный треугольникABC (AC = BC)  разрезать требуемым образом нельзя.   Очевидно, что существует два существенно различных способа разрезания треугольника на три: соединить внутреннюю точкуXс вершинами (рис. слева) или разрезать треугольник на два прямой, проходящей через вершину, а затем повторить эту операцию с одной из двух частей (рис. справа).  В первом случае треугольникAXBможет быть равнобедренным только при  AX = BX,  но тогда два других треугольника равнобедренными не будут. Во втором случае хотя бы один из получающихся при первом разрезе треугольников должен быть равнобедренным. Следовательно, первая прямая либо является биссектрисой прямого угла, либо соединяет точкуCс точкойDна гипотенузе, для которой  AD = AC.  Ни в том, ни в другом случае провести вторую прямую так, чтобы получить нужное разрезание невозможно.

Только прямоугольный равнобедренный треугольник.