Назад

Олимпиадная задача по планиметрии о вписанном четырёхугольнике (8-9 класс)

Задача 203913 • Сложность: 2 • 8-9 класс
Задача

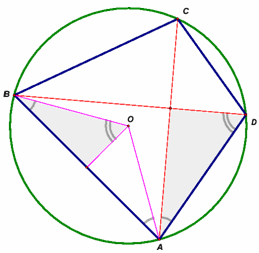
Четырёхугольник ABCD вписан в окружность, центр O которой лежит внутри него.

Доказать, что, если  ∠BAO = ∠DAC,  то диагонали четырёхугольника перпендикулярны.

Авторы:
Заславский А. А.
Разделы:
Планиметрия
Источники:
I Олимпиада по геометрии имени И.Ф. Шарыгина (2005 г.) 9 класс Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина
Количество версий:
4
Решение

Так как  ∠BAO = ½ (π – ∠AOB) = π/2 – ∠ADB,  то  ∠DAC + ∠ADB = π/2,  что равносильно утверждению задачи (см. рис.).

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет