Олимпиадная задача: Наименьшее число солдат в полку – задача Федорова Р. М.
Задача
В честь праздника 1% солдат в полку получил новое обмундирование. Солдаты расставлены в виде прямоугольника так, что солдаты в новом обмундировании оказались не менее чем в 30% колонн и не менее чем в 40% шеренг. Какое наименьшее число солдат могло быть в полку?
Решение
Оценка. Пусть m – число колонн, а n – число шеренг. Тогда в полку mn солдат и 1/100 mn солдат получили новое обмундирование. Согласно условию, не менее чем в 40/100 n шеренг есть хотя бы по одному солдату в новом обмундировании, значит, mn/100 ≥ 40n/100. Отсюда m ≥ 40. Аналогично
mn/100 ≥ 30m/100, откуда n ≥ 30. Значит, в полку не менее, чем 40·30 = 1200 солдат.
Пример. Построим 1200 солдат в виде прямоугольника 30×40
Поставим по диагонали 12 солдат в новом обмундировании (см. рисунок). Ясно, что солдаты в новом обмундировании стоят ровно в 30% колонн и в 40% шеренг. 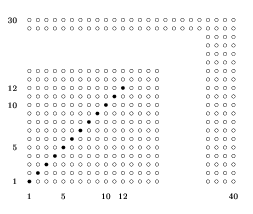
Ответ
1200 солдат.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь