Олимпиадная задача Спивака по планиметрии и комбинаторной геометрии, 2 уровень
Задача
Отметьте на плоскости 6 точек так, чтобы от каждой на расстоянии 1 находилось ровно три точки.
Решение
Нарисуем равносторонний треугольник со стороной 1 и сдвинем его ''вверх'' (или в любую другую сторону, только не под углом 60oк стороне) на 1 (см. рисунок). Вершины этих двух треугольников мы и отмечаем: они удовлетворяют условию задачи. Догадаться до этого решения можно так. Сделаем из проволоки два равносторонних треугольника со стороной 1. Расположим их в пространстве один над другим на расстоянии 1 и соединим соответствующие вершины проволокой (получается так называемая треугольная призма). Теперь ''аккуратно положим'' этот проволочный каркас на плоскость.
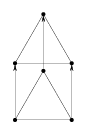
Ответ
См. рисунок.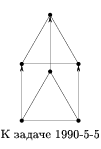
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет