Задание олимпиады по планиметрии: сравнение площадей в квадрате для 7–8 классов
Задача
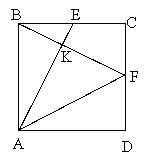
Сравнение площадей.Точки E и F — середины сторон BC и CD квадрата ABCD. Отрезки AE и BF пересекаются в точке K. Что больше: площадь треугольника AKF или площадь четырехугольника KECF?
Решение
Пусть 4S — площадь квадрата. Тогда площадь каждого из треугольников ABE, ADF, BCF равна S, поэтому площадь треугольника ABF равна 2S. Но треугольник AKB — часть треугольника ABE, поэтому его площадь меньше S, а это означает, что площадь треугольника AKF больше S. С другой стороны, площадь четырехугольника KECF меньше S, т.к. он составляет часть треугольника BCF.
Ответ
Площадь треугольника больше.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет