Олимпиадная задача: доказательство целостности многочлена для 7–9 классов
Задача
Целое число.Доказать, что если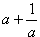 - целое число, то
- целое число, то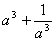 - тоже целое число.
- тоже целое число.
Решение
Перепишем формулу сокращенного умножения для куба суммы (k + n)3 = k3 + n3 + 3kn(k + n)
илиk3 + n3 = (k + n)3 − 3kn(k + n). Теперь можем записать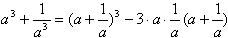 . Справа стоит целое число, следовательно, выражение слева — целое.
. Справа стоит целое число, следовательно, выражение слева — целое.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет