Олимпиадная задача Сендерова: доказательство неполного квадрата числа a0…09
Задача
Докажите, что число вида a0...09 – не полный квадрат (при любом числе нулей, начиная с одного; a – цифра, отличная от 0).
Решение
Для n = 1 утверждение проверяется непосредственно.
Пусть n > 1 и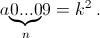 
Тогда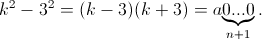 
Разложим 
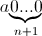на простые множители; в разложении получится
n + 1 множитель 2, n + 1 множитель 5 и все множители числа a. Числа k – 3 и k + 3 не могут оба делиться на 5, значит, все множители 5 содержатся либо в k – 3, либо в k + 3, а остальные множители как-то распределены между k – 3 и k + 3. Следовательно, разность между этими числами не менее 5n+1 – 9·2n+1 > 6 при n > 1. Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет