Олимпиадная задача: Периодичность числовой последовательности и рациональность x₁
Задача
Бесконечная последовательность чисел xn определяется условиями: xn+1 = 1 – |1 – 2xn|, причём 0 ≤ x1 ≤ 1.
а) Докажите, что последовательность, начиная с некоторого места, периодическая в том и только в том случае, когда x1 рационально.
б) Сколько существует значений x1, для которых эта последовательность – периодическая с периодом T (для каждого T = 2, 3, ...)?
Решение
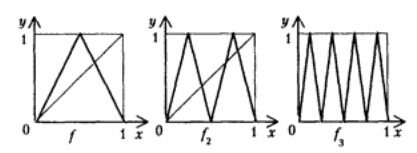
а) См. задачу 198221. б) Положим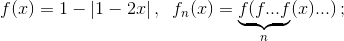 
графики функций y = f(x), y = f2(x) и y = f3(x) показаны на рисунке.
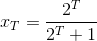(ясно, что при k < T все решения уравнения x = fk(x) меньшеxT). Взяв в качествеx1тот из двух прообразовxT при отображении x→f(x), которыйне входитв "периодическую траекторию", порождаемуюxT, мы получим последовательность, которая, начиная со второго места, – периодическая с периодомT. Эту последовательность, в свою очередь можно нарастить спереди и т.д.
Ответ
б) Бесконечное число.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет