Олимпиадная задача Егорова А. А.: Алгебраическое неравенство для 8–10 классов

Решение 1:Предположим, что  a² + b² < 8.  Тогда согласно неравенству Коши – Буняковского (см. задачу 161402)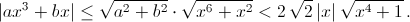  

Следовательно,  x⁴ + ax³ + 2x² + bx + 1 > 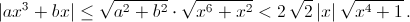  Противоречие.

Решение 2:Пусть t – корень уравнения. Тогда   0 = t⁴ + at³ + 2t² + bt + 1 = t²(t + ^a/₂)² + (1 + ^bt/₂)² + t²(2 – ^a²+b²/₄).   Поскольку  t ≠ 0,  то  ^a²+b²/₄ < 2.

Ответ задачи отсутствует