Олимпиадная задача по последовательностям: докажите бесконечность полных квадратов
Задача
Числовая последовательность определяется условиями: 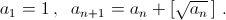
Докажите, что среди членов этой последовательности бесконечно много полных квадратов.
Решение
Заметим, что если an = m² + k, где 1 ≤ k ≤ m, то an+1 = m² + m + k, а an+2 = m² + 2m + k = (m + 1)² + k – 1, то есть "излишек" над квадратом уменьшается на 1.
Если теперь as = m², то as+1 = m² + m, as+3 = (m + 1)² + m – 1, ..., as+2m+1 = (2m)² = 4m², то есть следующий квадрат в 4 раза больше предыдущего. Так как a1 = 1, то в последовательность попадают квадраты вида 4k и только они.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет