Олимпиадная задача: Сумма n чисел и их квадраты — доказать ограничение произведения

Решение 1:Пусть  x₁ ≤ x₂ ≤ ... ≤ x_n  – данные числа. Тогда  (x₁ – x_k)(x_n – x_k) ≤ 0  при каждом k от 1 до n. Сложив все эти неравенства, получим

nx₁x_n – (x₁ + x_n)·0 + 1 ≤ 0,  то есть  x₁x_n ≤ – ¹/_n.

Решение 2:Рассмотрим на плоскости n точек с координатами 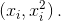   По условию координаты их центра тяжести равны  (0, ¹/_n).  Тем самым, найдётся точка с положительной абсциссой. Проведём через точку с наибольшей положительной абсциссой и центр тяжести прямую. Эта прямая пересекает параболу

y = x²  ещё в одной точке, абсциссу которой обозначим u. Поскольку все остальные точки не могут лежать ниже этой прямой, найдётся точка с абсциссой

x_j ≤ u.  Заметим, что x_i и u удовлетворяют уравнению  ¹/_n + kx = x²,  значит, их произведение  ux_i = – ¹/_n,  а  x_ix_j ≤ – ¹/_n.

Ответ задачи отсутствует