Олимпиадная задача Воронина: Оборот карт в колоде и минимизация операций

  a) Обозначим карты цифрами. Пусть вначале они упорядочены по убыванию:  9, 8, 7, 6, 5, 4, 3, 2, 1.  Покажем результаты перекладываний, выделяя подчёркиваниями переложенные карты:

  б) Обозначим карты числами от 1 до 52, предположим, что сначала они упорядочены по убыванию. Поменяем местами половины колоды, получим:  26, 25, ..., 2, 1, 52, 51, ..., 27.  Теперь выделенную пару карт перенесём в конец:  26, 25, ..., 2, 51, 50, ..., 27, 1, 52.  Очередную пару на стыке двух исходных половинок врежем в уже перенесённые в конец карты:  26, 25, ..., 3, 50, 49, ..., 27, 1, 2, 51, 52,  а далее продолжаем этот процесс. Последней будет перенесена пара 26, 27, после чего колода оказывается упорядоченной по возрастанию. Всего потребовалось  1 + 26 = 27  операций.   в) По-прежнему считаем, что в начале карты упорядочены по убыванию. Беспорядком назовём пару стоящих рядом карт, если номер левой больше номера правой. Первоначально имеется 51 беспорядок. При каждом вынимании части колоды мы можем уничтожить не более двух беспорядков (разрушаем две соседние пары), а при вставке в колоду разрывается только одна пара, так что можем уничтожить не более одного беспорядка. Это показывает, что меньше, чем 17 операциями не обойтись. Но и 17 операций недостаточно, поскольку на первом шаге при вынимании число беспорядков уменьшается не более чем на 1: если мы вынимаем часть, расположенную с краю, то при этом разрывается только одна пара, а если вынимаем из середины, то возникает один новый беспорядок во вновь образовавшейся паре соседних карт.   г) Докажем, что при каждой операции число беспорядков уменьшается не более чем на 2, а при первой и последней операции – на 1. Тогда 26 операций хватит, чтобы уничтожить  1 + 24·2 + 1 = 50  беспорядков, а в начале их – 51.

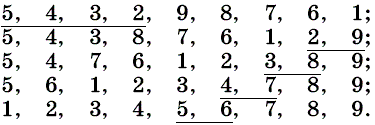
  Допустим, что при некоторой операции число беспорядков уменьшилось на 3. Это означает, что при вынимании исчезло два беспорядка и ни один не возник, а при вставке исчез один и ни один не возник. Пусть вынимается кусок с первой картой a и последней b и вставляется между картами e и f:

Сформулированные условия означают, что  c < d,  c > a,  b > d,  следовательно,  b > a.  С другой стороны,  e > f,  e < a,  b < f,  то есть  a > b.  Полученное противоречие доказывает невозможность уничтожения трёх беспорядков за одну операцию.

  Докажем, что на первом шаге число беспорядков не может уменьшиться на 2. Если вынимаем с краю, то рвём только один беспорядок, а если изнутри, то два уничтожаем, а один возникает. Если после этого вынутый кусок ставим с краю, то число беспорядков не уменьшается, а если вставляем внутрь, то один беспорядок уничтожается, но другой возникает.   Аналогично рассматривается последний шаг.

Ответ задачи отсутствует