Олимпиадная задача Фомина: пары натуральных чисел с условием для дробей
Задача
Сколько существует таких пар натуральных чисел (m, n), каждое из которых не превышает 1000, что 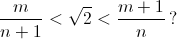
Решение
Рассмотрим все пары (m, n) натуральных чисел, для которых m + n + 1 = s ≥ 3. Имеем 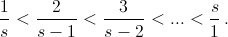 Поскольку s > 2 >
Поскольку s > 2 > ![]() > ½ > 1/s, а число
> ½ > 1/s, а число ![]() иррационально, оно попадает ровно в один из указанных интервалов. Таким образом, среди пар (m, n) с фиксированным значением s найдётся ровно одна, для которой выполняются указанные в условии неравенства. При этом точка пересечения
иррационально, оно попадает ровно в один из указанных интервалов. Таким образом, среди пар (m, n) с фиксированным значением s найдётся ровно одна, для которой выполняются указанные в условии неравенства. При этом точка пересечения ![]() прямых y =
прямых y = ![]() x и y + x = s попадает в квадрат с вершинами (m, n), (m + 1, n), (m, n + 1), (m + 1, n + 1). Нас интересуют пары (m, n), у которых оба числа не превосходят 1000, то есть должны выполняться неравенства
x и y + x = s попадает в квадрат с вершинами (m, n), (m + 1, n), (m, n + 1), (m + 1, n + 1). Нас интересуют пары (m, n), у которых оба числа не превосходят 1000, то есть должны выполняться неравенства 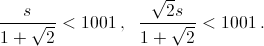 Отсюда
Отсюда 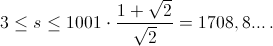 Всего таких значений s, а значит, и пар 1706.
Всего таких значений s, а значит, и пар 1706.
Ответ
1706 пар.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь