Задача
Дана невозрастающая последовательность неотрицательных чисел a1 ≥ a2 ≥ a3 ≥ ... ≥ a2k+1 ≥ 0.
Докажите неравенство: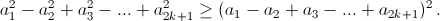 
Решение
Рассмотрим трапецию, ограниченную прямыми x = a2k, x = a2k–1, y = 0, y = 2x (см. рисунок).
, следовательно, выражение в левой части неравенства равно сумме площадей всех трапеций и треугодьника, в который вырождается последняя трапеция. Сдвинув все трапеции влево до упора, мы получим ступенчатую фигуру, содержащую треугольник (ограниченный прямыми x=a1–a2+a3–a4+ ... +a2k+1, y= 0, y= 2x), площадь которого равна выражению в правой части (см. рисунок).
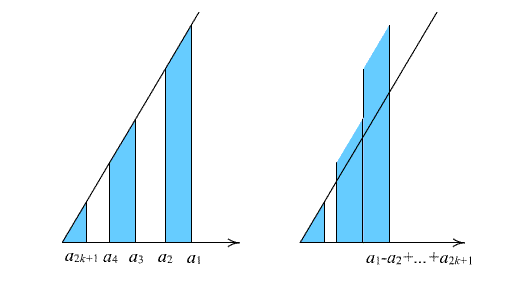
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет