Рассмотрим некоторую сторону многоугольника. Будем считать её вертикальной. Построим цепочку параллелограммов, в которой каждый следующий находится правее предыдущего и примыкает к нему по вертикальной стороне. Цепочка начинается на левой стороне многоугольника, а кончается на правой. Она обязана пересекаться с любой аналогичной цепочкой, соединяющей горизонтальные (верхнюю и нижнюю) стороны многоугольника. Общий элемент таких цепочек – прямоугольник. Каждой паре перпендикулярных направлений сторон многоугольника соответствует по крайней мере один такой прямоугольник.

  Далее можно считать, что параллелограммы примыкают друг к другу целыми сторонами (в противном случае можно произвести дополнительное разрезание – параллелограмм П режется на более мелкие, стороны которых параллельны сторонам П; в частности, все прямоугольники разрежутся на более мелкие и их суммарная площадь не изменится). Теперь каждой паре вертикальной и горизонтальной цепочек соответствует ровно один прямоугольник (поскольку по прямоугольнику цепочки однозначно восстанавливаются), и его площадь равна произведению отрезков сторон многоугольника, породивших эти цепочки.

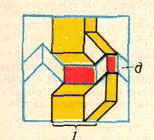
  Всего получаем не менее k прямоугольников с суммой площадей ka².

ka².