Задача
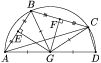
В выпуклом четырёхугольнике ABCD точки E, F и G – середины сторон AB, BC и AD соответственно, причём GE ⊥ AB, GF ⊥ BC. Найдите угол ACD.
Решение
Так как каждый из отрезков GE и GF является одновременно высотой и медианой в треугольниках AGB и BGC соответственно (см. рис.), то
DG = AG = BG = CG. Следовательно, G – центр окружности, описанной около данного четырёхугольника. ∠ACD = 90°, так как это вписанный угол, опирающийся на диаметр окружности.
Ответ
90°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет