Задача
Доказать, что при любой расстановке знаков "+" и "−" у нечётных степеней x выполнено неравенство
x2n ± x2n–1 + x2n–2 ± x2n–3 + ... + x4 ± x³ + x² ± x + 1 > ½ (x – произвольное действительное число, а n – натуральное).
Решение
Достаточно доказать, что 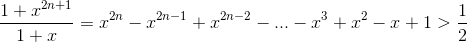 для любого положительногоx. Если x≥ 1, то, очевидно, левая часть не меньше 1; если же x< 1, то знаменатель не превосходит 2, и дробь больше ½.
для любого положительногоx. Если x≥ 1, то, очевидно, левая часть не меньше 1; если же x< 1, то знаменатель не превосходит 2, и дробь больше ½.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет