Задача
Доказать, что при любых x >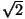 
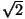и y > выполняется неравенство x4 – x³y + x²y² – xy³ + y4 > x² + y².
Решение
Левая часть равна 
. Поскольку х > 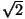и у > 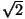, то x5 + y5 > 2(x³ + y³) и > 2
= 2(x² − xy + y²) ≥ x² + y².
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет