Заметим, что обратное утверждение доказать значительно проще: если в многоугольник можно вписать окружность, то при отодвигании всех его сторон на одно и тоже расстояние (в частности, на единицу) получается подобный многоугольник, причём центром подобия служит центр окружности. Перейдём теперь к решению задачи. Первый способ. 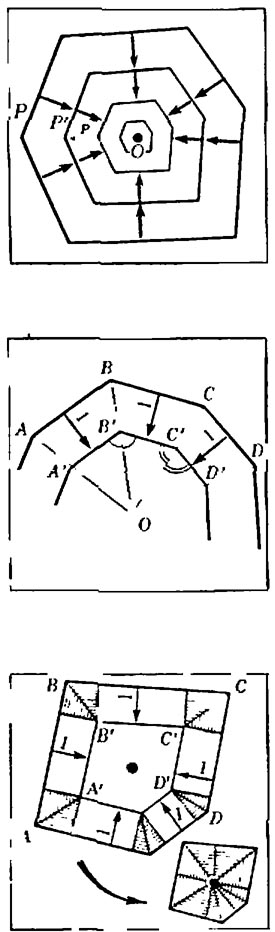Пусть многоугольникP' получается из многоугольникаPотодвиганием сторон внутрь многоугольникаPна расстояние 1 и в то же времяP' можно получить изPпреобразованиемfподобия с коэффициентомk< 1. Подвергнем этому преобразований многоугольникPвместе с нарисованным внутри него многоугольникомP'. Тогда внутриP' (образаP) появится новый многоугольникP'' (образP'), подобныйP' (с коэффициентомk) иP(с коэффициентомk²), причём, очевидно, стороныP'' =f(P') можно получить отодвиганием сторонP'внутрь на расстояниеk. Точно так же, отодвинув стороны ещё наk²получим многоугольникf(P'') =P⁽³⁾, расположенный внутриP'' (образP'' при преобразованииf), и так далее:f(P⁽³⁾) =P⁽⁴⁾,...,f(P⁽ⁿ⁾) =P⁽ⁿ⁺¹⁾, ..., гдеP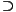P'P'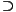'P⁽³⁾...P⁽ⁿ⁾.... Очевидно, поскольку стороны многоугольникаP⁽ⁿ⁾каждый раз уменьшаются в одном и том же отношении, их длины стремятся к нулю, и поэтому пересечение всех многоугольников состоит из одной точки. (Тот факт, что это пересечение не пусто, легко вывести из аналогичного утверждения для числовой прямой: последовательность вложенных отрезков [a;b][a₁;b₁]...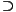[a_n,b_n]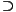... всегда имеет общую точку (это утверждение или какое-либо ему эквивалентное при аксиоматическом введении действительных чисел принимается обычно за аксиому).) Обозначим её черезO. Каждая сторона многоугольникаP' последовательно отодвигается на расстоянияk,k²,k³,...,kⁿ,..., поэтому расстояние от каждой стороны до точкиOравно одному и тому же числу — сумме бесконечной геометрической прогрессии

Таким образом, окружность с центромOи радиусомrкасается всех сторон многоугольникаP'. Заметим, что в приведённом доказательстве было несущественно, какие именно стороны соответствуют друг другу при преобразовании подобияf, переводящемPвP'. Можно доказать такуюлемму: если многоугольникиPиP' (полученный изPотодвиганием сторон на 1) подобны с каким угодно соответствием сторон (с "поворотом" или "симметричным отражением" порядка сторон), то всегда будет иметь место и подобие c естественным порядком сторон — гомотетия с коэффициентомk(0 <k< 1). Доказательство, независимое от первого решения, мы приведём в конце, а пока дадим ещё два решения задачи, опирающихся на эту лемму (то есть подразумевающих естественное соответствие сторон при подобии).

Второй способ.Пусть [AB] — сторонаP, [A'B'] — соответствующая сторонаP',O — точка пересечения (AA') и (BB'). Тогда

Отсюда следует, что в той же точкеOпрямуюBB' пересекает прямаяCC' (BCиB'C' — соответствующие стороныPиP'), и так далее. Кроме того, очевидно, что прямыеAA',BB',CC',... являются биссектрисами угловA',B',C',... многоугольникаP'. Отсюда следует, что точкаOслужит центром окружности, вписанной вP'.

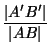Третий способ.Разрежем "щель" между многоугольникамиPиP' на прямоугольники высоты 1 с основаниямиA'B',B'С',С'D', ... и "ромбоиды" — четырёхугольники, остающиеся у каждой вершиныA,B,C, .... Очевидно, из этих ромбоидов можно составить один многоугольник, описанный около окружности радиуса единица, причём его углы соответственно конгруэнтны$\angle$A,$\angle$B,$\angle$C,..., а длины сторон равны разностям длин соответствующих сторон многоугольниковPиP', то есть равны (1 −k)|AB|, (1 −k)|BC|, .... Таким образом, наш многоугольникP' подобен многоугольнику, описанному около окружности радиуса 1, значит, и в него можно вписать окружность (радиус её будет равен, очевидно,r=${\frac{k}{1-k}}$).

Доказательство леммы.Будем для каждой стороны [AB] многоугольникаPобозначать через [A'B'] ту сторонуP', которая получается при отодвиганииAB. Пусть при подобии стороне [A₁B₁] соответствует [A₂'B₂']: [A₁B₁]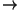[A₂'B₂'], [A₂B₂]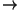[A₃'B₃'], ..., [A_r-1B_r-1]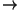[A_r'B_r'], [A_rB_r]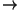[A₁'B₁']. Тогда$\angle$A₁=$\angle$A₂= ... =$\angle$A_r= 2α и$\angle$B₁=$\angle$B₂= ... =$\angle$B_r= 2β, а поэтому разность длин |A_iB_i| − |A_i'B_i'| =dодна и та же для всехi(d=ctgα +ctgβ). Пустьk — коэффициент подобия, |A_iB_i| =x_i. Тогда

Но, как нетрудно доказать, это система (при 0 <k< 1) имеет только одно решениеx₁=x₂= ... =x_r=${\frac{d}{1-k}}$. Таким образом, мы доказали, что для любой стороныA₁B₁многоугольникаP|A₁'B₁'| =k|A₁B₁|, то есть соответствующие друг другу (при отодвигании!) стороны многоугольников пропорциональны. Углы при отодвигании не меняются, поэтому подобие многоугольников с естественным соответствием сторон [AB]$\to$[A'B'] доказано.

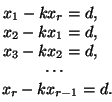
Ответ задачи отсутствует