Задача
Дана плоскость P и две точки A и B по разные стороны от неё. Построить сферу, проходящую через эти точки, высекающую из P наименьший круг.
Решение
Рассмотрим произвольную сферу, проходящую через точки A и B. Проведём через точку M пересечения отрезка AB и плоскости P диаметр CD окружности, являющейся пересечением данной сферы с плоскостью P. По свойству хорд MC·MD = MA·MB. Поэтому произведение чисел MC и MD не зависит от выбора сферы.
Минимум суммы двух чисел при фиксированном произведении достигается в случае, когда они равны, то есть MC = MD = 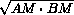 .
.
Ответ
Центр искомой сферы находится в точке M пересечения отрезка AB и плоскости P, а её радиус равен 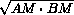 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет