Решение 1:Шар нужно пустить параллельно ближайшей к точке "малой" диагонали 2n-угольника (см. рис.). 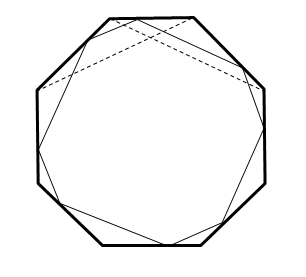Ясно, что в этом случае траектория шара замкнется (она представляет собой полуправильный 2n-угольник). Из подобия легко следует, что независимо от начальной точки сумма длин двух последовательных сторон полученного многоугольника равна "малой" диагонали исходного. Значит, и длина всего пути не зависит от начальной точки.

Решение 2:Каждый раз, когда шар отражается от некоторой стороны, будем отражать весь наш многоугольник относительно этой стороны и смотреть на продолжение движения шара в новом многоугольнике. Тем самым траектория шара распрямится. После 2n таких отражений мы получим многоугольник, который получается из исходного композицией 2n осевых симметрий. Эта композиция является параллельным переносом (композиция двух симметрий относительно соседних сторон – поворот на угол ^2π/_n). "Распрямлённая" траектория шара представляет собой отрезок, соединяющий две точки, получающиеся друг из друга этим переносом. Поэтому длина траектории равна длине вектора этого параллельного переноса, а её угол наклона к борту бильярда равен углу между этим вектором и стороной многоугольника, то есть он определен однозначно. Таким образом, есть только один способ выпустить шар в соответствии с условиями задачи (точнее, два – в одном случае он "обходит" стороны по, а в другом – против часовой стрелки). Он указан в решении 1.

Шар нужно пустить под углом ^π/_2n к борту.