Назад
Задача 178269 • Сложность: 3 • 10-11 класс
Задача

Доказать, что для любых трёх бесконечных последовательностей натуральных чисел

a1... an ...
b1... bn ...
c1... cn ...
найдутся такие номераpиq, что
ap$\displaystyle \ge$aq, bp$\displaystyle \ge$bq, cp$\displaystyle \ge$cq.
Разделы:
Последовательности Принцип крайнего
Источники:
Московская математическая олимпиада 1961 год 10 класс, 2 тур Олимпиады и турниры
Количество версий:
4
Решение

Докажем сперва, что из любой последовательности натуральных чисел можно выбрать неубывающую подпоследовательность, т. е. такую, что каждый её член не меньше предыдущего.

Пустьx1,x2,...,xn, ... — произвольная последовательность натуральных чисел. Так как все члены последовательности неотрицательны, то среди них существует наименьший — пусть это будет хр. Если среди членовхр + 1,xp + 2,..., следующих за хр, число, равное хр, встречается бесконечно много раз, то, выбрав все такие члены, мы уже получим требуемую подпоследовательность. Если же таких членов лишь конечное число, то выберем их все. Из идущей после последнего выбранного члена (равного хр) части последовательности снова выберем наименьшее числоxp1(оно, очевидно, будет больше хр) и все члены, равныеxp1, и так далее; получим неубывающую последовательность:

xp, xp,..., xp, xp1, xp1,..., xp1, xp2,....

Перейдём к решению задачи. Выберем из последовательностиa1,a2,...,an,... неубывающую подпоследовательность:
a'1, a'2,..., a'n,....
Из соответствующей последовательностиb'1,b'2,...,b'n,...:
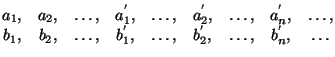
$\displaystyle \begin{matrix}a_{1}, &a_{2},&\dots, &a^{'}_{1}, &\dots, &a^{'}_{... ...&\dots, &b^{'}_{1}, &\dots, &b^{'}_{2},&\dots,&b^{'}_{n}, & \dots \end{matrix}$
в свою очередь выберем неубывающую подпоследовательность:
b''1, b''2,..., b''n,...
Наконец, выберем неубывающую подпоследовательность из соответствующей последовательностиc''1,c''2,...,c''n,...:
c'''1, c'''2, l..., c'''n,....
Рассмотрим теперь подпоследовательности
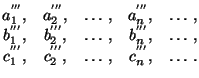
$\displaystyle \begin{matrix} a^{'''}_{1},& a^{'''}_{2},&\ldots,&a^{'''}_{n}, &... ...,\\ c^{'''}_{1},& c^{'''}_{2},&\ldots,&c^{'''}_{n}, & \ldots . \end{matrix}$
Все они не убывают (по построению) и, значит, для любыхp,q(р >q) имеют место неравенства:
a'''p$\displaystyle \ge$a'''q,    b'''p$\displaystyle \ge$b'''q,    c'''p$\displaystyle \ge$c'''q.
Мы, таким образом, доказали даже больше, чем требовалось в задаче.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет