Задачи и олимпиады по математике

Задача

Дан треугольникA₀B₀C₀. На его сторонахA₀B₀,B₀C₀,C₀A₀взяты точкиC₁,A₁,B₁соответственно. На сторонахA₁B₁,B₁C₁,C₁A₁треугольникаA₁B₁C₁взяты соответственно точкиC₂,A₂,B₂, и вообще, на сторонахA_nB_n,B_nC_n,C_nA_n, треугольникаA_nB_nC_nвзяты точкиC_{n + 1},A_{n + 1},B_{n + 1}. Известно, что

$\displaystyle {\frac{A_0B_1}{B_1C_0}}$ = $\displaystyle {\frac{B_0C_1}{C_1A_0}}$ = $\displaystyle {\frac{C_0A_1}{A_1B_0}}$ = k,$\displaystyle {\frac{A_1B_2}{B_2C_1}}$ = $\displaystyle {\frac{B_1C_2}{C_2A_1}}$ = $\displaystyle {\frac{C_1A_2}{A_2B_1}}$ = $\displaystyle {\frac{1}{k^2}}$

и вообще,

Доказать, что треугольникABC, образованный пересечением прямыхA₀A₁,B₀B₁,C₀C₁, содержится в треугольникеA_nB_nC_nпри любомn.

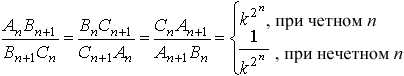
Решение

То, что треугольникABCсодержится в треугольникеA₁B₁C₁, очевидно. Покажем, что точкиA₂,B₂,C₂являются точками пересечения сторон треугольникаA₁B₁C₁с прямымиA₀A₁,B₀B₁,C₀C₁. Поместим в точкиA₀,B₀,C₀массы 1 +k³,k,k². Центром масс этой системы является точка пересечения отрезковA₀A₁иB₁C₁. Действительно,C₁— центр масс точекA₀иB₀с массами 1 иk,B₁— центр масс точекA₀иC₀с массамиk³иk²,A₁— центр масс точекB₀иC₀с массамиkиk². Таким образом, еслиA'— точка пересечения отрезковA₀A₁иB₁C₁, тоB₁A':A'C₁= (1 +k) : (k²+k³) = 1 :k², поэтомуA'=A₂. Для точекB₂иC₂доказательство аналогично.

Доказанный результат означает следующее. Для треугольникаA₁B₁C₁мы делаем то же самое, что и для треугольникаA₀B₀C₀, лишь с заменой коэффициентаkна 1/k²; треугольникABCпри этом остаётся тем же самым. Полученный треугольникA₂B₂C₂снова содержит треугольникABCи т.д.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления