Точка O лежит внутри выпуклого n-угольника A₁...A_n и соединена отрезками с вершинами. Стороны n-угольника нумеруются числами от 1 до n, разные стороны нумеруются разными числами. То же самое делается с отрезками OA₁, ..., OA_n.

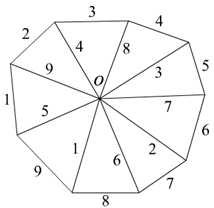
  а) При  n = 9  найти нумерацию, при которой сумма номеров сторон для всех треугольников A₁OA₂, ..., A_nOA₁ одинакова.

  б) Доказать, что при  n = 10  такой нумерации осуществить нельзя.