Пусть  f(x) = ax² + bx + c. Тогда 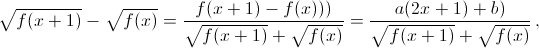    поэтому  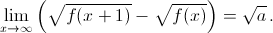   При целом x число  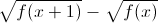   является целым, поэтому  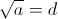   – целое число. Кроме того, найдётся такое натуральное x₀, что при целых  x ≥ x₀  разность  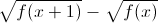   равна своему предельному значению d. Положим  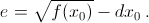   Тогда     при всех целых  x ≥ x₀.  Таким образом,  ax² + bx + c = (dx + e)²  для всех целых  x ≥ x₀.  Но тогда это равенство имеет место для всех x.

Ответ задачи отсутствует