Задача
Доказать, что если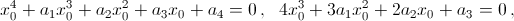 
то x4 + a1x³ + a2x² + a3x + a4 делится на (x – x0)².
Решение
Пусть f(x) = x4 + a1x³ + a2x² + a3x + a4. По условию f(x0) = f'(x0) = 0. Следовательно, x0 – двукратный корень многочлена f(x), то есть многочлен f(x) делится на (x – x0)².
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет