Будем поочерёдно проводить диагонали. Когда мы проводим новую диагональ, число частей, на которые проведённые ранее диагонали делят многоугольник, увеличивается на  m+ 1,  гдеm– число точек пересечения новой диагонали с ранее проведёнными (точки пересечения делят диагональ на отрезки, каждый из этих отрезков делит одну из старых частей на две "новых"). Таким образом, каждая новая диагональ и каждая новая точка пересечения диагоналей увеличивают число частей на 1. Поэтому общее число частей, на которые диагонали делятn-угольник, на единицу больше суммы числа диагоналей (оно равно  ½n(n– 3),  см. задачу60391) и числа точек пересечения диагоналей (оно равно 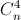 ,  см. задачу134981).

На   ¹/₂₄ n(n – 1)(n – 2)(n – 3) + ½ n(n – 3) + 1   частей.