Задача
Обозначим через Tk(n) сумму произведений по k чисел от 1 до n. Например, T2(4) = 1·2 + 1·3 + 1·4 + 2·3 + 2·4 + 3·4.
а) Найдите формулы для T2(n) и T3(n).
б) Докажите, что Tk(n) является многочленом от n степени 2k.
в) Укажите метод нахождения многочленов Tk(n) при k = 2, 3, 4, ... и примените его для отыскания многочленов T4(n) и T5(n).
Решение
а) 2T2(n) = (1 + ... + n)2 – (12 + ... + n2) =
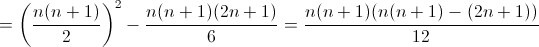
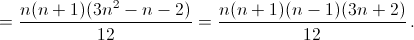
T3(n) находится аналогично из равенства
6T3(n) = (1 + ... + n)3 – 3(12 + ... + n2)(1 + ... + n) + 2(13 + ... + n3) =
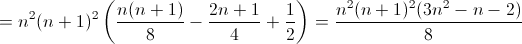
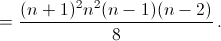
(Формулы для сумм квадратов и кубов см. в задачах 160282, 161431.)
б) Разобьем все слагаемые суммы Tk(n) на две группы: в одну включим те произведения, в которые входит n, в другую – остальные. Отсюда
Tk(n) – Tk(n–1) = nTk–1(n–1) (*).
Теперь утверждение доказыаается по индукции.
База.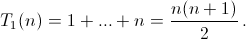 
Шаг индукции. По предположению индукции nTk–1(n–1) – многочлен степени 2k– 1 отn. Теперь из задачи161434следует, что существует многочлен степени 2k, значения которого совпадает сTk(n) при всех натуральныхn.
в) Полученная выше рекуррентная формула () и очевидное равенство Tk(k) =k! позволяют последовательно вычислять многочленыTk(n): формулу () можно рассматривать как систему уравнений на коэффициенты многочленаTk.
Чтобы уменьшить число неизвестных, заметим, что значениямногочлена Tkимеют смысл не только при натуральных n≥k, но и при всех целых (и даже действительных)n. Глядя на формулы дляT1,T2,T3, разумнопредположить, что
Tk(k–1) =Tk(k–2) = ... =Tk(1) =Tk(0) =Tk(–1) = 0.
Это предположение не противоречит рекуррентной формуле.
Например, будем искатьT4(n) в виде (n+ 1)n(n– 1)(n– 2)(n– 3)P(n), где P(n) =an3+bn2+cn+d. Выписав (*) для k= 4 и сократив на n(n– 1)(n– 2)(n– 3), получим
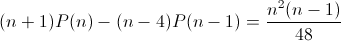или 48(n+ 1)(an3+bn2+cn+d) – 48(n– 4)(a(n– 1)3+b(n– 1)2+c(n– 1) +d) =n2(n– 1).
Далее можно приравнять коэффициенты при одинаковых степенях (например, сравнивая коэффициенты приn3, получим
48(a+b+ 4a+ 3a–b) = 1, откуда a=1/384).
Или можно подставлять "малые" значенияn. Например, при n= 1 получим соотношение 2a+ 2b+ 2c+ 5d= 0.
Продолжая таким образом, найдем указанное в ответе выражение дляT4. Аналогично находитсяT5.
Ответ
а)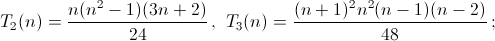 
в)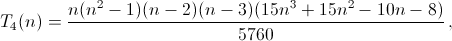 
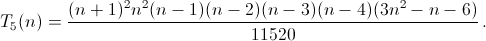
Чтобы оставлять комментарии, войдите или зарегистрируйтесь