Задача
n отрезков A1 B1 , A2 B2 , ... , An Bn (рис. 5) расположены на плоскости так, что каждый из них начинается на одной из двух данных прямых, оканчивается на другой прямой, и проходит через точку G (не лежащую на данных прямых) — центр тяжести единичных масс, помещенных в точках A1 , A2 , ... , An . Докажите, что
+
+...+
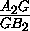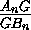=n.
Решение
Мы немного обобщим формулировку данной задачи, именно, будем считать, что в точках Ai находятся не единичные массы, а массы mi (точка G – центр тяжести масс mi , расположенных в точках Ai ). Докажем, что тогда
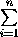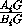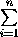mi 
= mi.
Поместим в каждую из точек Bi массу Mi=mi .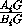
Тогда центр тяжести пары точек Bi и Ai (для всех i ) будет находиться
в точке G . Мы предполагаем, что не все точки A1 , ... , An лежат
на одной прямой (для удобства обозначим наши прямые буквами l1 и l2 ).
Центр тяжести точек Ai , лежащих на прямой l1 , обозначим через C1 ;
соответственно центр тяжести точек Ai , находящихся на l2 , обозначим
через C2 . Аналогично, центр тяжести точек Bi , лежащих на прямой lk
( k= 1, 2), обозначим через Dk . Соответствующие массы обозначим P(C1),
P(C2), P(D1), P(D2).
Из условия задачи следует, что центр тяжести точек C1 и C2 будет в точке G . С другой стороны, из выбора масс Mi следует, что центр тяжести точек C1 и D2 будет также в точке G . Поэтому должно быть P(C2)=P(D2). Аналогично получаем P(C1)=P(D1); значит,
P(C1)+P(C2)=P(D1)+P(D2).
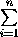mi , а P(D1)+P(D2)=
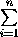Mi , т.е.
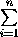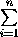mi=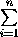 Mi= mi
,
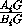Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь