Задача
Для любого натурального числа n сумма 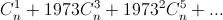 делится
делится
Решение
Обозначим нашу сумму через sn. Будем вести индукцию по n.
База. s1 = 1 делится на 20, s2 = 2 делится на 21.
Шаг индукции. Обозначим 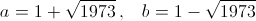 и заметим, что
и заметим, что 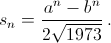
Поскольку an – bn = (an–1 – bn–1)(a + b) – ab(an–2 – bn–2) = 2(an–1 – bn–1) + 1972(an–2 – bn–2), то и sn = 2sn–1 + 4·493sn–2.
По предположению индукции sn–1 кратно 2n–2, sn–2 кратно 2n–3; значит, sn делится на 2n–1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет