Задача
Докажите, что если
а) a, b и c – положительные числа, то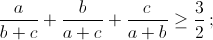 
б) a, b, c и d – положительные числа, 
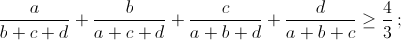в) a1, ..., an – положительные числа (n > 1), то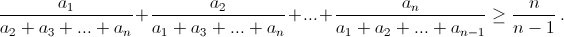 
Решение
в). Обозначим s = a1 + a2 + ... + an, bi = s – ai. Нам нужно доказать, что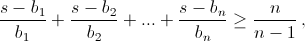 
то есть что
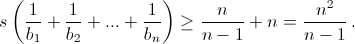Первый способ. Согласно неравенству между средним арифметическим и средним гармоническим (см. задачу 161402 в)
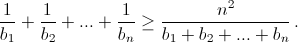
Но b1 + b2 + ... + bn = ns – a1 – a2 – ... – an = (n – 1)s, откуда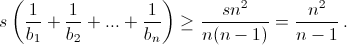 
Второй способ. 
Преобразуем так же остальные слагаемые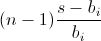 
и все n слагаемых сложим. Потом сгруппируем попарно дроби bi/bj и bj/bi и воспользуемся неравенством bi/bj + bj/bi ≥ 2.
Поскольку всего таких пар будет 
то в результате получим: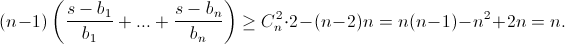 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь