Общая сумма всех стоящих в квадрате чисел равна  17·16 : 2 = 34·4;  суммы чисел, стоящих в строках, равны между собой, следовательно, сумма чисел, стоящих в каждой строке, столбце или диагонали, равна 34.

  Поэтому нам нужно доказать, что в квадратах, удовлетворяющих нашему условию, сумма чисел, симметричных относительно центра, равна 17. Будем считать, что 1 стоит в верхнем левом углу, а 16 – в правом нижнем, тогда два других числа на этой же диагонали – обозначим их через a и a' – удовлетворяют равенству  a + a' = 17.  Условимся всегда число, дополняющее число x до 17, обозначать через x':  x' = 17 – x.

  Воспользуемся обозначениями, приведенными на рисунке (S_i обозначают суммы чисел в соответствующих клетках).

  Сложив суммы чисел в двух средних столбцах, двух средних строках и дважды по второй диагонали, получим S₁+S₂+S₃+S₄+ 2(b + e) + 4(c + d) = 34·6.   Сложив суммы чисел в первой и четвёртой строке и в первом и четвёртом столбцах, получим  S₁+S₂+S₃+S₄+ 2(17 +b + e) = 34·4.   Вычитая, получим, что  4(c + d) = 34·2.  Значит,  c + d= 17,  а поэтому и  b + e= 17.   Перейдём теперь к следующему рисунку.  Ясно, что  y ≠ x',  поскольку  b≠ 16.  Заметим, чтоx'илиy'не могут попасть на одноцветные клетки; если эти клетки – красные, то, складывая числа в первой строке и первом столбце, мы получим, что  34·2 = 3·17 + 2,  а если эти клетки – жёлтые, то, складывая числа в первой строке и четвёртом столбце, мы получим, что  34·2 = 3·17 + 2b  – оба эти равенства неверны.   Пустьx'  стоит в красной клетке (случай, когда в нее попадаетy', разбирается аналогично), второе число в красной клетке обозначим черезz. Тогда, складывая число в первой строке и в первом столбце, получим  34 · 2 = 2 + 34 +y + z,  откуда  y + z= 32,  что невозможно.   Таким образом, ниx', ниy'не может попасть в красную клетку, а вместе они не могут попасть в жёлтые клетки. Значит, либоx', либоy'стоит на местеuилиv. Пусть этоx'  (случай, когда туда попадаетy', разбирается аналогично). Но  x' ≠ u,  поскольку  a ≠ c,  значит,  x' = v,  тогда  y' = u.   Аналогично доказывается утверждение задачи для чисел, стоящих в жёлтых и красных клетках.

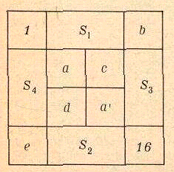
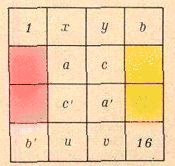
Ответ задачи отсутствует