а) В первом походе количество мальчиков было меньше ⅔ количества девочек – участниц этого похода. Тем более оно меньше ⅔ общего количества девочек – учениц класса. То же верно для мальчиков – участников второго похода. Поскольку каждый ученик был хотя бы в одном походе, всего мальчиков в классе меньше ⁴/₃ количества девочек. Следовательно, мальчиков в этом классе не больше ⁴/₇ общего числа учеников.   б) Пусть b_i и g_i – число мальчиков и девочек в i-м походе, b и g – число мальчиков и девочек на общей встрече. По условию  b_i = α_i(b_i + g_i),  откуда  (1 – α_i)b_i = α_ig_i ≤ α_ig,  поэтому если все  α_i < 1,  то 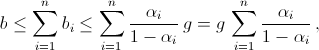    откуда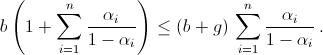  

  Итак, если  α_i < 1  для всех i, то мальчики будут составлять не более 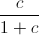    от общего числа участников походов, где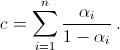  

  Докажем, что эта граница может достигаться. Для этого требуется, чтобы все написанные неравенства превратились в равенства. Легко понять, что это будет так, если девочки во всех походах были одни и те же, а мальчики – разные, то есть каждый из мальчиков был только в одном походе. Покажем, что это может быть при любых α_i. Пусть 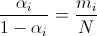    (числа α_i и, следовательно,  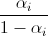   рациональны; мы можем записать  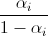   в виде дробей с одним и тем же знаменателем). Тогда, если в i-м походе N (одних и тех же) девочек и m_i (разных) мальчиков, то на встречу придут  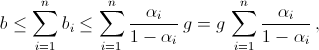   мальчиков и N девочек; отношение M к N как раз равно c, а отношение M к  M + N  равно    .

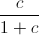  Если же  α_j = 1  для некоторого j (хотя бы для одного), то мы уже не можем дать никакой отличной от 1 оценки сверху для доли мальчиков на общей встрече. Действительно, если взять число участников j-го похода очень большим (все они – мальчики), то долю мальчиков на общей встрече можно сделать сколь угодно близкой к 1.

Ответ задачи отсутствует