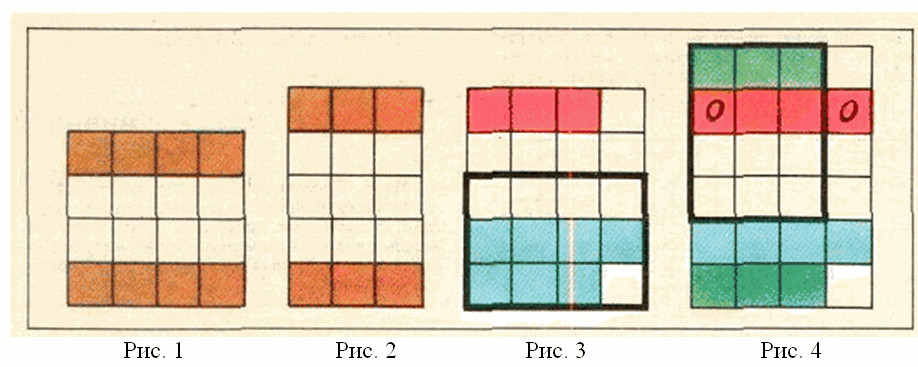
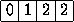Предположим, что нам удалось заполнить лист клетчатой бумаги требуемым образом. Заметим, что в двух закрашенных на рис.1 прямоугольниках
поровну нулей, поровну единиц и поровну двоек, поскольку они дополняются одной
и той же фигурой до прямоугольника 3×4. По той же причине этих чисел в прямоугольниках, закрашенных на рис. 2. Докажем ряд утверждений о расположении нулей, единиц и двоек.
1. В прямоугольнике 1×3 не более одного нуля.
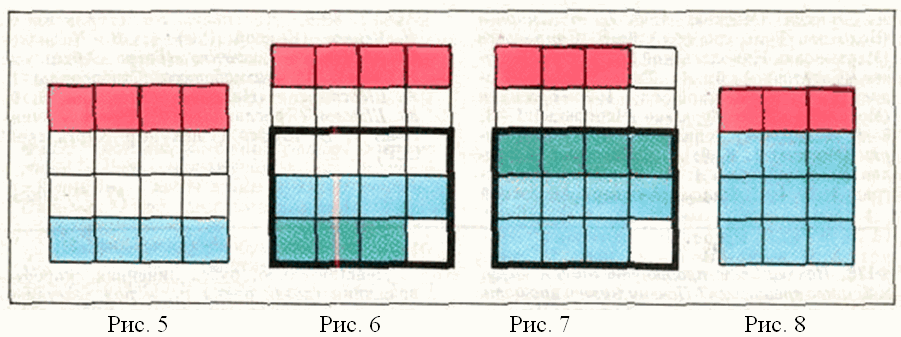
Действительно, если в красном прямоугольнике 1×3 на рис. 3 более
одного нуля, то более одного нуля в каждом из двух голубых прямоугольников
1×3 и 1×4. В то же время оба голубых прямоугольника входят
в один прямоугольник 3×4, в котором должно быть три нуля.
2. В прямоугольнике 1×4 не более одного нуля.
Если в красном прямоугольнике 1×4 на рис. 4 два нуля, то они
расположены именно так, как показано на рисунке. Два нуля должно быть
и в голубом прямоугольнике и, следовательно, по одному нулю в каждом из
зелёных прямоугольников. Но тогда в двух прямоугольниках 1×4,
расположенных между красным и голубым прямоугольниками, нулей нет (иначе
нашёлся бы прямоугольник 3×4 более чем с тремя нулями). Следовательно, в обведённом прямоугольнике 3×4 лишь два нуля.
3. В прямоугольнике 1×4 не менее одного нуля.
Если в красном прямоугольнике 1×4 на рис. 5 нет нулей, то нет
их в голубом прямоугольнике. Следовательно, в двух прямоугольниках 1×4 между ними должно быть три нуля. В то же время в каждом из этих прямоугольников не более одного нуля.
Таким образом, в каждом прямоугольнике 1×4 ровно один нуль.
4. В прямоугольнике 1×4 не более двух единиц.
Если в красном прямоугольнике 1×4 на рис. 6 более двух единиц, то
более двух единиц в голубом прямоугольнике 1×4 и не менее двух –
в зелёном прямоугольнике 1×3. Но тогда найдётся прямоугольник 3×4, содержащий больше четырёх единиц.
5. В прямоугольнике 1×4 не более двух двоек.
Если в красном прямоугольнике 1×4 на рис. 6 больше двух двоек, то
больше двух двоек в голубом и не менее двух – в зелёном прямоугольнике.
В прямоугольнике 1×4, расположенном над голубым прямоугольником, есть хотя бы одна двойка, так как в нем не более двух единиц и один нуль.
Следовательно, в обведённом прямоугольнике 3×4 больше пяти двоек.
6. В прямоугольнике 1×3 не более одной единицы.
Если в красном прямоугольнике 1×3 на рис. 7 две единицы, то по две
единицы в голубых прямоугольниках 1×4 и 1×3. Так как в зелёном прямоугольнике есть единица (в нем не более двух двоек и один нуль), то в обведённом прямоугольнике 3×4 больше четырёх единиц.
7. В прямоугольнике 1×3 не менее одной единицы.
Если в красном прямоугольнике 1×3 на рис. 8 нет ни одной единицы,
то поскольку в каждом из голубых прямоугольников не более одной единицы, в прямоугольнике 3×4 оказывается лишь три единицы.
Таким образом, в каждом прямоугольнике 1×3 ровно одна единица.
Возьмём какой-нибудь нуль. Рядом с ним есть единица, так как в противном случае нашелся бы прямоугольник 1×3 без единиц. Так как в прямоугольнике 1×4 должен быть один нуль, а в прямоугольнике 1×3 – одна единица, то две следующие клетки занимают двойки:
В следующей за двойками клетке должен находиться как нуль, так и единица, так как иначе найдётся соответственно или прямоугольник 1×4 без нулей, или прямоугольник 1×3 без единиц. Противоречие.