Задача
Для каждого натурального n > 1 существует такое число cn, что для любого x произведение синуса числа x, синуса числа x + π/n, синуса числа
x + 2π/n, ..., наконец, синуса числа x + (n – 1)π/n равно произведению числа cn на синус числа nx. Докажите это и найдите величину cn.
Решение
sin nx = sin x·Un–1(cos x), где Un–1 – многочлен Чебышёва (см. задачу 161099). Из рекуррентных соотношений задачи 161100 следует, что Un–1 – многочлен степени n – 1 с первым коэффициентом 2n–1.
Положим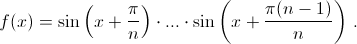 
Сгруппируем попарно члены вида 
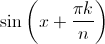и 
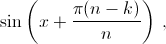где
0 < k < n/2. Если n чётно, то в произведении останется ещё член 
Преобразуем попарные произведения: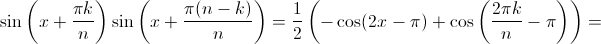 
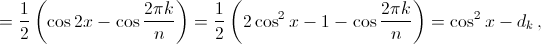где di – некоторые константы.
Итак, f(x) = Dn(cos x), где Dn(x) – некоторый многочлен степени n – 1 с первым коэффициентом 1.
Осталось доказать, что Un–1(x) = 2n–1Dn(x) (в частности, отсюда будет следовать, что константа cn в условии равна 21–n).
Рассмотрим многочлен F(x) = Un–1(x) – 2n–1Dn(x). Его степень меньше n – 1, так как коэффициенты при xn–1 у многочленов Un–1(x) и 2n–1Dn(x) равны.
Рассмотрим точки xk = – πk/n (k = 1, ..., n – 1) и пусть tk = cos xk. Ясно, что f(xk) = 0, и потому Dn(tk) = 0; кроме того, sin (nxk) = 0,
а sin xk ≠ 0, – значит, Un–1(cos xk) = Un–1(tk) = 0.
Заметим, что все точки tk различны, так как cos x возрастает на отрезке [– π, 0].
Итак, многочлен F(x) обращается в нуль в n – 1 точке t1, t2, ..., tn–1 и, значит, F(x) – тождественный нуль. Таким образом, Un–1 = 2n–1Dn, то есть 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь