Задача
а) В ведро налили 12 литров молока. Пользуясь лишь сосудами в 5 и 7 л, разделите молоко на две равные части.
б) Решите общую задачу: при каких a и b можно разделить пополам a + b литров молока, пользуясь лишь сосудами в a литров, b литров и a + b литров? За одно переливание из одного сосуда в другой можно вылить всё, что там есть, или долить второй сосуд до верха.
Решение
а) См. таблицу:
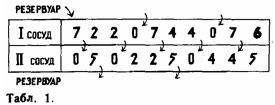
Обозначим через dk "остаток" от деления ka на b (k = 1, 2, 3, ...): dk = ka – lkb, 0 ≤ dk < b.
Нам достаточно доказать, что можно получить dm литров. Действительно, поскольку dm = ma – lmb – наименьшее неотрицательное число вида ma + lb, где l – целое, то, добавляя к dm еще l + lm порций по b литров, мы сможем получить нужное количество с ma + lb литров. Как получить dm литров, ясно из таблиц 2 (для m > 0) и 3 (для m < 0).
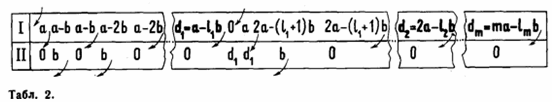
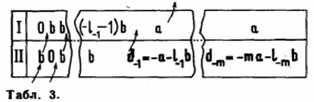
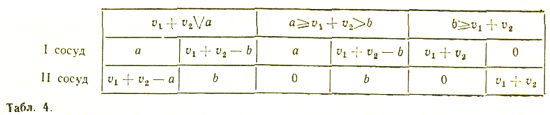
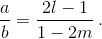
Ответ
Если a/b рационально, причём числитель и знаменатель соответствующей несократимой дроби нечётны.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь