Задача
Для любых n вещественных чисел a1, a2, ..., an существует такое натуральное k ≤ n, что каждое из k чисел ak, ½ (ak + ak–1),
⅓ (ak + ak–1 + ak–2), ..., 1/k (ak + ak–1 + ... + a2 + a1) не превосходит среднего арифметического c чисел a1, a2, ..., an.
Решение
Предположим противное: существуют такие вещественные числа a1, a2, ..., an, что для каждого k (1 < k ≤ n) найдётся такое l (1 ≤ l < k), что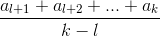 
больше среднего арифметического c всех этих чисел.
В частности, найдётся такое n1, что среднее арифметическое чисел от an1+1 до an больше c. Возьмём теперь k = n1; для него найдётся такое n2 (0 ≤ n2 < n1), что среднее арифметическое чисел от an2+1 до an1 больше c; если n2 > 0, то найдём но нему n3, и т.д. до тех пор, пока некоторое nr+1 не окажется нулём, то есть очередное среднее арифметическое будет браться от a1 до anr. Так как среднее арифметическое в каждой группе больше c, то и среднее арифметическое всех чисел больше c. Но c – среднее всех n чисел. Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь