Примем прямую l за ось Ox , а точку O – за начало координат прямоугольной системы, как показано на рис.5. Единица масштаба уже задана в условии. Сетка линий, о которой идет речь в условии, составлена из окружностей радиуса n с центром O (уравнение такой окружности x²+y²=n² ) и прямых y=m , где m и n – всевозможные целые числа; n>0. Таким образом, каждой точке пересечения (или касания) этих линий– каждому "узлу"(x,y)нашей сетки– соответствует определенная пара значений n=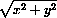 и m=y . Заметим, что когда мы переходим от одной из розовых точек к соседней розовой точке, то и m , и n изменяются на единицу, так что их разность n-m=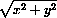-y остается постоянной; эта разность для всех розовых точек равна6.

Уравнение 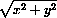-y=6эквивалентно следующим: x²+y²=(y+6)² ; y=x²/12-3. Таким образом, все розовые точки лежат на параболе y=x²/12-3.

В другой подобной цепочке точек, которую мы нарисовали голубым цветом, при переходе от точки к соседней 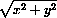и y меняются на единицу так, что постоянной остается их сумма: 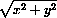+y=4. Это уравнение после преобразований тоже превращается в уравнение параболы y=-x²/6+3/2.

Точно так же можно показать, что любая бесконечная цепочка точек, в которой соседние точки являются противоположными вершинами одной клетки (или одного сегмента), лежит на параболе y=-x²/2p+ p/2, где p – некоторое целое число, отличное от нуля. Обратно, на любой из этих парабол лежит такая бесконечная цепочка точек (это точки пересечения параболы со всевозможными прямыми y=m ).

Заметим, что если p<0, т.е. если ветви параболы уходят вверх, то при четном p парабола идет по темным клеткам, а при нечетном p – по желтым; если же p>0, то наоборот. При этом через каждую точку пересечения прямых и окружностей нашей сетки (исключая точки касания, лежащие на прямой x=0), проходят две параболы; одна идет по желтым клеткам, другая– по темным; одна направлена ветвями вверх, другая– вниз.

По существу, решение задачи M68 очень близко к доказательству эквивалентности геометричского и алгебраического определений параболы.

Ответ задачи отсутствует