Решение 1:Так как  BP² = BQ² = BA·BC',  а четырёхугольники AC'A'C и AB'A'B (AA' – третья высота) вписанные, получаем, что

CP·CQ = CB² – BP² = CB² – BA·BC' = BC² – BC·BA' = BC·CA' = CA·CB'.  Это, очевидно, равносильно утверждению задачи.

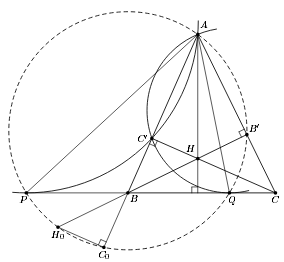
Решение 2: Пусть точка C₀ симметрична C' относительно B. Тогда  BC₀·BA = BC'·BA = BP² = BP·BQ,  то есть точки A, P, Q, C₀ лежат на одной окружности ω. Пусть H₀ – точка этой окружности, диаметрально противоположная A. Тогда  H₀C₀ ⊥ AB.  Поэтому точка, симметричная H₀ относительно B (то есть середины PQ), лежит на высоте CC'; кроме того, она лежит на высоте AA' треугольника APQ (поскольку средняя линия треугольника AH₀A', параллельная AA', проходит через центр ω, а значит, и через точку B). Значит, точка H₀ симметрична ортоцентру H треугольника ABC относительно B. Поэтому  BH₀·BB' = BH·BB' = BC'·BA = BC₀·BA,  что и означает, что B' также лежит на ω (см. рис.).

Ответ задачи отсутствует