Задача
Дан выпуклый четырёхугольник ABCD. Пусть ωA, ωB, ωC, ωD – описанные окружности треугольников BCD, ACD, ABD, ABC соответственно. Обозначим через XA произведение степени точки A относительно ωA на площадь треугольника BCD. Аналогично определим XB, XC, XD. Докажите, что XA + XB + XC + XD = 0.
Решение
Для вписанного четырёхугольника утверждение очевидно (все степени равны нулю).
Заметим, что точка D лежит вне окружности ωD тогда и только тогда, когда ∠A + ∠C > ∠B + ∠D, то есть тогда и только тогда, когда C лежит внутри окружности ωC. Таким образом, знаки чисел XC и XD противоположны.
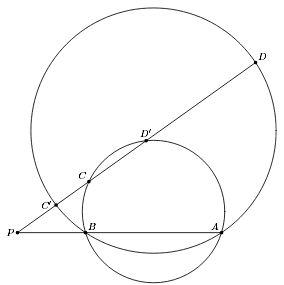
Пусть прямая CD пересекает AB в точке P, а окружности ωC, ωD повторно – в точках C′, D′. Тогда отношение площадей треугольников ABC и ABD равно отношению их высот, которое, в свою очередь, равно PC/PD. Поскольку PC·PD′ = PA·PB = PC′·PD, это отношение равно
PC′/PD′ = PC–PC′/PD–PD′ = CC′/DD′. С другой стороны, отношение абсолютных значений степеней точек C и D относительно соответствующих окружностей равно CD·CC′/CD·DD′ = CC′/DD′ (см. рис.). Следовательно, |XC| = |XD| и XC + XD = 0.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь