Задача
В прямоугольном треугольнике ABC точка D – середина высоты, опущенной на гипотенузу AB. Прямые, симметричные AB относительно AD и BD, пересекаются в точке F. Найдите отношение площадей треугольников ABF и ABC.
Решение
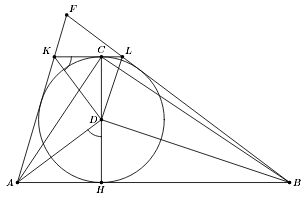
Пусть CH – высота треугольника, K, L – точки пересечения прямой, проходящей через C параллельно AB, с AF и BF соответственно (см. рис.). Так как трапеция AKLB описана около окружности с диаметром CH, то KD и LD – биссектрисы углов AKL и BLK соответственно. Поэтому
∠CKD = 90° – ∠HAD, то есть треугольники KCD и DHA подобны, а KC = CD²/AH = CH²/4AH = BH/4. Аналогично CL = BH/4.
Ответ
4 : 3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет