Задача
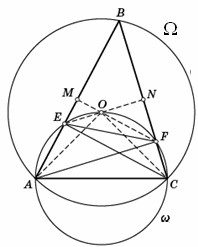
Точка O – центр описанной окружности Ω остроугольного треугольника ABC. Описанная окружность ω треугольника AOC вторично пересекает стороны AB и BC в точках E и F. Оказалось, что прямая EF делит площадь треугольника ABC пополам. Найдите угол B.
Решение
Пусть ∠B = β. Тогда ∠AOC = 2β. Первый способ. ∠AEC = ∠AOC = 2β, ∠ECB = ∠AEC – ∠B = β, то есть треугольник CEB – равнобедренный. Аналогично треугольник ABF – равнобедренный.
Следовательно, AB = 2BF cos β и BC = 2BE cos β. Перемножив, получим AB·BC = 4BE·BF cos²β. По условию 4cos²β = AB·BC/BE·BF = SABC/SBEF = 2. Так как 2β < 180°, то 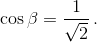
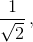 так как SBFE = ½ SABС , а SBMN = ¼ SABС.
так как SBFE = ½ SABС , а SBMN = ¼ SABС.
Ответ
45°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет