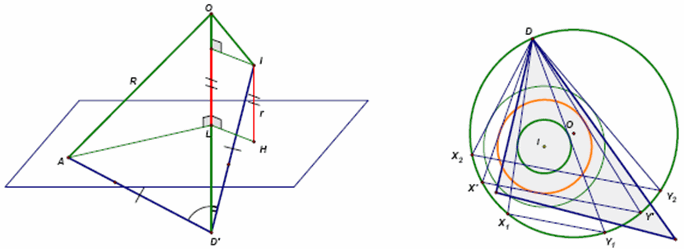
Пусть R, r – радиусы описанной и вписанной сфер тетраэдра ABCD,  О – центр его описанной сферы, L – центр описанной окружности треугольника АВС,  Н – проекция I на плоскость АВС. Из условия следует, что О и D' лежат на перпендикуляре к плоскости АВС, проходящем через L, поэтому прямые DO' и IH параллельны (рис. слева). Кроме того,  D'A = D'I  (как радиусы описанной сферы тетраэдра IABC),  OA = R,  IH = r.

  Дважды применим теорему косинусов – к треугольникамAD'OиOD'I:  R² =D'A² +D'O² – 2D'A'·D'Ocos∠AD'O,  OI²=D'I² +D'O² – 2D'I·D'Ocos∠ID'O.   Отсюда  R² –OI² = 2D'O·|D'Acos∠AD'O – D'Icos∠ID'O| = 2D'O·IH.   Следовательно,  D'O=¹/_2r(R² –OI²).   Аналогично доказывается, что и точкиA', B', C'удалены отОна такое же расстояние.   Таким образом, описанные сферы тетраэдровABCDиA'B'C'D'концентричныиD'O– радиус описанной сферы тетраэдраA'B'C'D'.   Докажем, что  D'O > R  ⇔  ¹/_2R(R² –OI²) >r.  Для этого проведём плоскостьDOI. Она пересекает описанную и вписанную сферу по окружностям с центрамиO, Iи радиусамиR, r, а тетраэдр – по некоторому треугольнику. ВершинаDэтого треугольника лежит на большей окружности, а из двух других вершин по крайней мере одна лежит внутри этой окружности. Кроме того, меньшая окружность целиком лежит внутри этого треугольника и внутри большей окружности. Поэтому, если провести черезDхордыDX₁иDY₁большей окружности, касающейся меньшей, то меньшая окружность окажется строго внутри треугольникаDX₁Y₁. Будем "раздувать" меньшую окружность, сохраняя центр и увеличивая радиус (рис. справа). Из соображений непрерывности следует, что наступит момент, когда "раздутая" окружность (некоторого радиусаr') будетвписанав треугольникDX'Y', образованный парой касательных с вершиной вD.   Этот же треугольник будетвписанв большую окружность, поэтому для него выполняетсяформула Эйлера:  OI² =R² – 2Rr'.   Следовательно,  r < r'=¹/_2R(R² –OI²).

Ответ задачи отсутствует