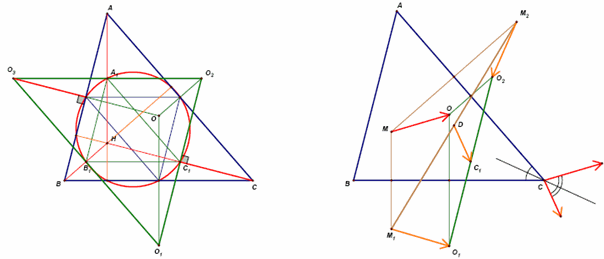
Пусть АВС – треугольник, образованный прямыми l_i, Н – его ортоцентр. Заметим, что середины О₁О₂, О₂О₃, О₃О₁ совпадают с серединами А₁, В₁, С₁ отрезков АН, ВН, СН и, стало быть, лежат на окружности девяти точек треугольника АВС. Действительно, стороны треугольника О₁О₂О₃ параллельны средним линиям треугольника АВС и вдвое больше их, поскольку переводятся друг в друга гомотетией с центром в О и коэффициентом 2 (рис. слева). Следовательно, треугольник О₁О₂О₃ центрально симметричен АВС. Значит, прямая, проходящая через точку С и середину О₁О₂, параллельна прямой, проходящей через О₃ и середину АВ, то есть совпадает с высотой треугольника АВС, а Н является центром гомотетии АВС и А₁В₁С₁.

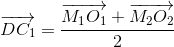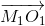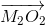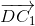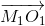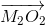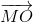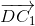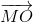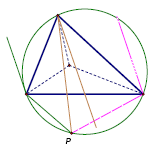
  ПустьD– серединаМ₁М₂. Тогда    и, так как    и    получаются друг из друга поворотом вокруг точкиСна угол 2∠С,    образует с каждым из них угол, равный 2∠С. Кроме того,    и    переходят в    при симметрии относительноСВиСАсоответственно, поэтому    и    образуют равные углы с биссектрисой углаС(а значит, равные углы и с биссектрисой углаС₁в треугольникеА₁В₁С₁).   Проведя аналогичные рассуждения для двух других середин, приходим к выводу, что прямые, соединяющиеА₁,В₁,С₁с серединами сторон треугольникаМ₁М₂М₃, симметричны относительно биссектрис треугольникаА₁В₁С₁прямым, проходящим черезА₁,В₁,С₁и параллельнымОМ.   Теорема. Тройка прямых, выходящих из вершин треугольника, пересекается в одной точке, расположенной на описанной окружности этого треугольника, тогда и только тогда, когда прямые, симметричные данным относительно биссектрис соответствующих углов, параллельны (см. рис.).  Доказательствоиспользует простой подсчет углов.   Согласно этой теореме, тройка прямых в нашей задаче пересекается на описанной окружности треугольникаА₁В₁С₁, то есть наокружности девяти точекисходного треугольника.

Ответ задачи отсутствует