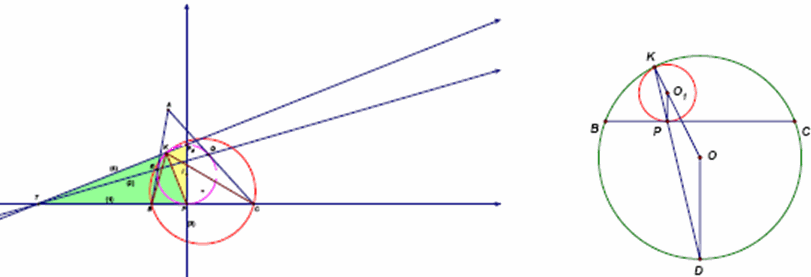
Задача
В треугольник АВС вписана окружность и отмечен её центр I и точки касания P, Q, R со сторонами ВС, СА, АВ соответственно. Одной линейкой постройте точку К, в которой окружность, проходящая через вершины В и С, касается (внутренним образом) вписанной окружности.
Решение
Сначала проведём прямую PI. Если она проходит через точку А, то АВ = АС, и К совпадает с точкой P', диаметрально противоположной точке Р.
Далее рассматриваем случай, когда АВ ≠ АС.
Построение (рис. слева).
1. Проведём прямую ВС.
2. Проведём прямую QR и отметим точку T пересечения этой прямой с прямой ВС.
3. Проведём прямую P'T и отметим точку К – вторую точку пересечения этой прямой с вписанной окружностью.
Точка К и есть искомая.
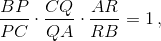а по теореме Менелая 
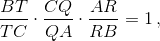следовательно, BP:PC = BT:TC.
Согласно решению задачи153599КР– биссектриса углаВКС(рис. справа). По свойству биссектрисы, BP/CP = KB/KC= λ ≠ 1.
Поэтому точкаКлежит на окружности Аполлония для отрезкаВСс отношением λ, построенной наРТкак на диаметре, то есть уголТКР– прямой, или, что то же, прямым является уголPKP', что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь