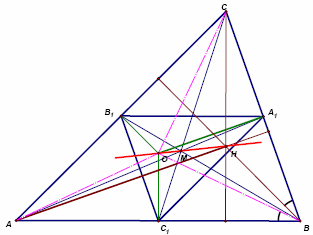
Пусть АВС – исходный треугольник, А₁, В₁, С₁ – середины сторон ВС, СА, АВ соответственно. Так как треугольники АВС и А₁В₁С₁ гомотетичны относительно точки М пересечения медиан (с коэффициентом −½), а центр О описанной окружности треугольника АВС является ортоцентром треугольника А₁В₁С₁, то точка М лежит на отрезке ОН (Н – ортоцентр треугольника АВС) и  НМ = 2МО.

  Поэтому, если центрIвписанной окружности не лежит на одной прямой (прямой Эйлера) с тремя остальными точками, то можно однозначно установить роль каждой из точек в треугольникеАВС. Отметим, что эта прямая проходит не более чем через одну вершину треугольника, так что можно считать, что точкиАиВне лежат на ней.   Итак,Iлежит на прямой Эйлера. Так как  ∠OBA= ∠HBC=^π/₂– ∠C, BIявляется биссектрисой углаНВО. Следовательно, точкаIлежит на отрезкеОН, причём  OI= 2IH  (иначе роль точек устанавливается однозначно). По свойству биссектрисы получаем, что  ВО= 2ВН.  Аналогично  АО= 2АН.  Таким образом,  AH = BH=^R/₂,  гдеR– радиус описанной окружности треугольникаАВС.   Из гомотетии, указанной выше, следует также, что  АH= 2OA₁  (и эти отрезки параллельны). Кроме того,  ОА₁=RcosA  (так как ∠OBA₁= ½ ∠BOC= ∠A).  Поэтому  ^R/₂=АН= 2RcosA  ⇒  cosA= ¼.   Точно так же доказывается, что  cosB= ¼.

arсcos ¼, arсcos ¼,  π – 2 arсcos ¼.